■

行列の積の計算は%*%を使う。

>  a <- matrix(1:4, 2, 2) 
> a
     [,1] [,2]
[1,]    1    3
[2,]    2    4
>  b <- matrix(0:3, 2, 2)    
> b
     [,1] [,2]
[1,]    0    2
[2,]    1    3
> a+b
     [,1] [,2]
[1,]    1    5
[2,]    3    7
> a%*%b
     [,1] [,2]
[1,]    3   11
[2,]    4   16
> a*b #これは要素ごとの積で行列の積ではない
     [,1] [,2]
[1,]    0    6
[2,]    2   12

リストとは、異なるデータ構造を集めて１つのオブジェクトにしたもの。
リスト形式にしたデータに、リストの要素そのものにアクセスするには の二重括弧を用いる。[ ]の括弧だとベクトルとしてのアクセスを行うことになる。

> x <- list(1:3, 4:6, 7:9) #要素数を揃える必要はない
> x
[[1]]
[1] 1 2 3

[[2]]
[1] 4 5 6

[[3]]
[1] 7 8 9

> x[[1]] #要素の取り出し
[1] 1 2 3


> x[1] #リストの要素番号まで取り出される
[[1]]
[1] 1 2 3

参考

■

大規模データ，比較的手が届くもののリスト．

• Wikipediaのダンプデータ

• 日本の統計サイト, e-Satマクロなやつ多し．

• TwitterのAPIを使って自分で集める．

• Mathematica提供のデータを使う．（Mathematicaのライセンスは必要．）

• NewmanグループのNetwork data

• Stanford Large Network Dataset Collection

• 無料で閲覧できる、たくさんの調査データのリンク集

• 大規模データを無料で手に入れることのできるサイトまとめ

• AmazonのPublic Data Sets(上記サイトで紹介されていたものの1つ)

• Data ARchives and Transmission System 宇宙の観測データ

• Time Series Data Library by Pro­fes­sor Rob J Hyn­d­man in DataMarket

• The Free 'Big Data' Sources Everyone Should Know まとめサイト発見．ただし，すでに知っているのも多い．(2015.01)

■

先頭が#で始まる行だけ出力。

awk '/^#/ {print $0}' test.txt 

先頭が#で始まらない行だけ出力。

awk '/^[^#]/ {print $0}' test.txt 

シェルの中でawkを実行して，その結果を変数として，次のコマンドへ渡す。
下の例ではresへawkの結果を書き込んで，$resとして次のコマンドへ渡している。

#!/bin/sh

res=`awk -f check1.awk -v word=$1 lex.csv`

echo "original:"$1

awk -f check2.awk -v res=$res lex.csv

■

先頭にゼロをつけて桁を揃える。

BEGIN{
}
{
    split($1,x,"-");
    str=sprintf("%4d-%02d-%02d",x[1],x[2],x[3]);
    print str,$2
}
END{
}

input : 2015-9-5 516773

output: 2015-09-05 516773

■

列方向のデータのソートを行う。
input : 999999 37705 55754
output: 37705 55754 999999

BEGIN{
FS = " "
}
{
for(k=1;k<=NF;k++){
    id[k] = $k
}

sort(id,NF)

for(k=1;k<=NF;k++){
   printf id[k]" "
}
printf"\n"
}
END{
}
function sort(ARRAY,ELEMENTS,tmp,i,j){
    for(i=2;i<=ELEMENTS;i++){
        for(j=i;(j-1) in ARRAY && ARRAY[j-1] > ARRAY[j];j--){
            tmp=ARRAY[j];
            ARRAY[j]=ARRAY[j-1];
            ARRAY[j-1]=tmp
        }
    }
    return
}

sed&awk プログラミング改訂版 (O'Reilly Japan)より。

■

RでDFAのチェック。

set.seed(1)
#White noise
eda.plot(DFA(rnorm(1500)))
#H~0程度

#Random walk
eda.plot(DFA(cumsum(rnorm(1500))))
#H~0.5程度

お手軽ランダムウォークはただ単にcumsum(rnorm(1500))，でよろしい。相関をチェックしたければacf(rnorm(1500))やacf(cumsum(rnorm(1500)))とすればよい。

■

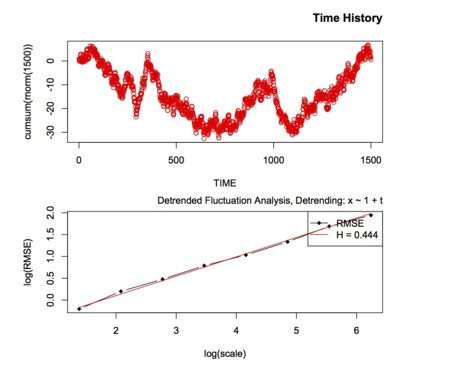
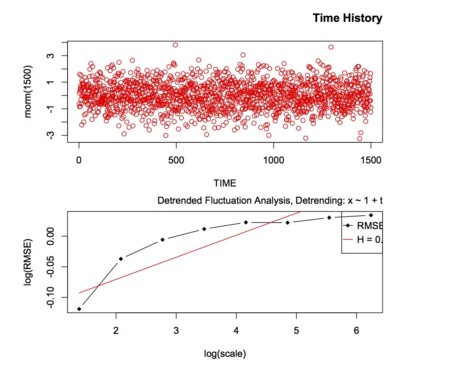
先日読んだ論文で使われていたDFAを試してみようとRのpackageをインストール。

install.packages("fractal", dependencies = TRUE)
library(fractal)

#正規乱数で試して見る
x <- DFA(rnorm(1024))
print(x)
eda.plot(x)

#正規乱数で試して見る，時間窓は1.1倍刻みで，途中の経過を表示
x <- DFA(rnorm(1024),scale.ratio=1.1,verbose=TRUE)
print(x)
eda.plot(x)

#結果のwindow sizeとresidualを取り出す。
attributes(x)
y <- paste(attr(x,"scale"),attr(x,"stat"),sep=",")
write.table(y,"test.csv",append=FALSE,quote=FALSE,row.names=FALSE,col.names=FALSE)

#結果のH指数を取り出す
z <- attr(x,"logfit")
write.table(z$coefficients[2],"test.csv",append=FALSE,quote=FALSE,row.names=FALSE,col.names=FALSE)

#window内を２次式で近似
z <- DFA(rnorm(1024),detrend="poly2",scale.ratio=1.1)
eda.plot(z)

「scale.ratio: the ratio of successive scales. This argument is used as an input to the logScale function. Default: 2.」なので，
scale.ratio=2だと，Scale 6.00000 12.00000 24.00000 48.000 96.0000 192.0000 384.00。
scale.ratio=1.1だと，Scale 6.0000 7.00000 8.0000 9.00000 10.00000 11.0000 12.000 14.0000 15.0000 17.00000 18.00000 20.00000 22.00000 25.00000 27.00000 30.00000 .... てな具合。